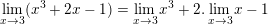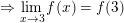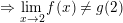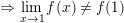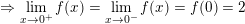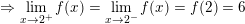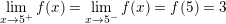Trong bài học trước các em đã biết về giới hạn của hàm số, thế nào là giới hạn hữu hạn, giới hạn một bên và giới hạn ở vô cực. Tiếp theo chúng ta sẽ tìm hiểu về hàm số liên tục trong nội dung bài học này.
Đang xem: Hàm số liên tục là gì
Bài viết dưới đây sẽ giúp ta biết cách xét tính liên tục của hàm số, vận dụng giải các dạng bài tập về hàm số liên tục như: Xét tính liên tục của hàm số tại 1 điểm (x=0), trên một đoạn hay một khoảng, tìm các điểm gián đoạn của hàm số, hay chứng minh phương trình f(x)=0 có nghiệm.
I. Lý thuyết về hàm số liên tục (tóm tắt)
1. Hàm số liên tục tại 1 điểm
– Định nghĩa: Cho hàm số y = f(x) xác định trên khoảng (a;b) và x0 ∈ (a;b). Hàm số y = f(x) được gọi là liên tục tại x0 nếu:
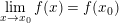
– Hàm số f(x0) không liên tục tại điểm x0 thì x0 được gọi là điểm gián đoạn của hàm số f(x).
2. Hàm số liên tục trên một khoảng
– Định nghĩa: Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.
– Hàm số y = f(x) được gọi là liên tục trên đoan
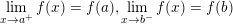
3. Một số định lý cơ bản về hàm số liên tục
• Định lý 1:
a) Hàm số đa thức liên tục trên toàn bộ tập số thực R.
b) Hàm số phân thức hữu tỉ (thương của 2 đa thức) và các hàm số lượng giác liên tục trên từng khoảng của tập xác định của chúng.
• Định lý 2:
– Giả sử f(x) và g(x) là hai hàm số liên tục tại điểm x0. Khi đó:
a) Các hàm số f(x) + g(x); f(x) – g(x) và f(x).g(x) liên tục tại x0.
b) hàm số
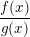
liên tục tại x0 nếu g(x0) ≠ 0.
• Định lý 3:
– Nếu hàm số y = f(x) liên tục trên đoạn
° Dạng 1: Xét tính liên tục của hàm số tại điểm x0.
* Phương pháp:
– Bước 1: Tính f(x0)
– Bước 2: Tính hoặc
– Bước 3: So sánh: hoặc với
rồi rút ra kết luận
– Nếu
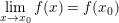
hoặc
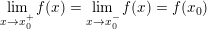
thì kết luận hàm số liên tục tại
– Nếu không tồn tại hoặc thì kết luận hàm số không liên tục tại x0.
– Bước 4: Kết luận.
* Ví dụ 1 (Bài 1 trang 140 SGK Đại số 11): Dùng định nghĩa xét tính liên tục của hàm số f(x)=x3 + 2x – 1 tại x0=3.
° Lời giải ví dụ 1 (Bài 1 trang 140 SGK Đại số 11):
– Ta có: f(x) = x3 + 2x – 1
⇒ f(3) = 33 + 2.3 – 1 = 32
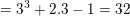
⇒ f(x) liên tục tại x0 = 3.
* Ví dụ 2 (Bài 2 trang 140 SGK Đại số 11): a) Xét tính liên tục của hàm số y = g(x) tại x0 = 2, biết:
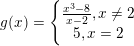
b) Trong biểu thức g(x) ở trên, cần thay số 5 bởi số nào đó để hàm số liên tục tại x0 = 2.
Xem thêm: Câu Lạc Bộ Là Gì ? Ý Nghĩa Của Từ Clb Phương Pháp Tổ Chức Hoạt Động Câu Lạc Bộ
° Lời giải ví dụ 2 (Bài 2 trang 140 SGK Đại số 11):
– Ta có: g(2) = 5.
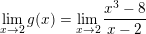
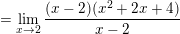
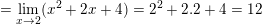
⇒ g(x) không liên tục tại x0 = 2.
b) Để g(x) liên tục tại x0 = 2 thì:
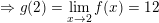
– Vậy chỉ cần thay 5 bằng 12 thì hàm số liên tục tại x0 = 2.
* Ví dụ 3: Xét tính liên tục của hàm số sau tại điểm x = 1.
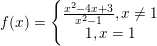
° Lời giải ví dụ 3:
– Ta có: f(1) = 1
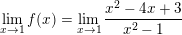
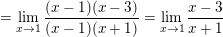
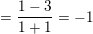
⇒ Vậy hàm số f(x) không liên tục (gián đoạn) tại điểm x = 1.
* Ví dụ 4: Xét tính liên tục của hàm số sau tại điểm x = 0.
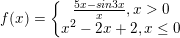
° Lời giải ví dụ 4:
– Ta có: f(0) = 02 – 2.0 + 2 = 2.
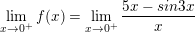
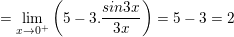
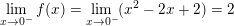
⇒ Vậy hàm số f(x) liên tục tại điểm x = 0.
° Dạng 2: Xét tính liên tục của hàm số trên một khoảng, một đoạn.
* Phương pháp:
– Áp dụng định lý 1, định lý 2 để xét tính liên tục của hàm số trên từng khoảng xác định của nó.
– Nếu hàm số xác định bởi 2 hoặc 3 công thức, ta thường xét tính liên tục tại các điểm đặc biệt của hàm số đó.
* Ví dụ 1: Cho hàm số
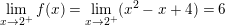
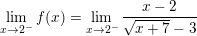
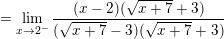
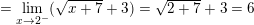
⇒ Hàm số f(x) liên tục tại điểm x = 2.
– Kết luận: Hàm số f(x) liên tục trên khoảng (-7;+∞).
* Ví dụ 2: Tìm a, b để hàm số sau liên tục:
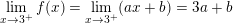
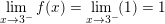
⇒ Để hàm số liên tục tại điểm x = 3 thì:
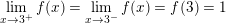
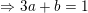
(*)
• Khi x = 5 thì f(5) = 5a + b
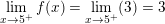
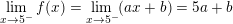
⇒ Để hàm số liên tục tại điểm x = 5 thì:
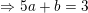
(**)
Từ (*) và (**) ta có:
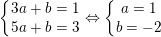
– Vậy khi a = 1 và b = -2 thì hàm số f(x) liên tục trên R, khi đó:
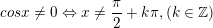
– Hàm số g(x) liên tục trên các khoảng:
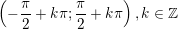
° Dạng 3: Tìm điểm gián đoạn của hàm số f(x)
* Phương pháp: x0 là điểm gián đoạn của hàm số f(x) nếu tại điểm x0 hàm số không liên tục. Thông thường x0 thỏa mãn một trong các trường hợp sau: