Lớp 1-2-3
Lớp 1
Lớp 2
Vở bài tập
Lớp 3
Vở bài tập
Đề thi
Lớp 4
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Lớp 5
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Lớp 6
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 7
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 8
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 9
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 10
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 11
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 12
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
IT
Ngữ pháp Tiếng Anh
Lập trình Java
Phát triển web
Lập trình C, C++, Python
Cơ sở dữ liệu

Công thức, Định nghĩa Toán, Lí, HóaĐường thẳngHình tam giácCác trường hợp tam giác bằng nhauHình thangHình bình hànhHình thoiHình chữ nhật
Trực tâm của tam giác là gì ? Định nghĩa, tính chất trực tâm tam giác chi tiết
Trang trước
Trang sau
•Trực tâm của tam giác là giao điểm của ba đường cao của tam giác đó.
Đang xem: Trực tâm của tam giác là gì
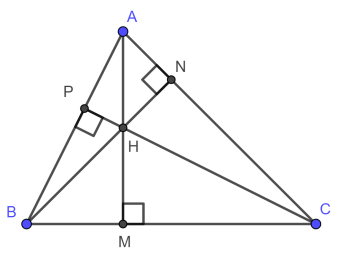
Tam giác ABC có ba đường cao là AM, BN, CP. Gọi H là giao điểm của ba đường cao trên thì H là trực tâm của tam giác ABC.
•Tính chất:
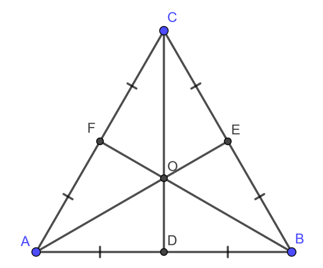
-Trong tam giác đều, trọng tâm, trực tâm, điểm cách đều ba cạnh, điểm nằm trong tam giác và cách đều ba cạnh là bốn điểm trùng nhau.
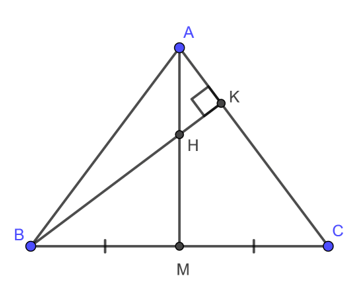
Ví dụ: Cho tam giác ABC cân tại A, đường trung tuyến AM và đường cao BK. Gọi H là giao điểm của AM và BK. Chứng minh rằng CH vuông góc với AB.
Hướng dẫn:
Vì tam giác ABC cân tại A nên đường trung tuyến AM cũng là đường cao của tam giác ABC.
Ta có H là giao điểm của hai đường cao AM và BK nên H là trực tâm của tam giác ABC
Suy ra CH là đường cao của tam giác ABC
Vậy CH vuông góc với AB.
Giới thiệu kênh Youtube honamphoto.com
CHỈ CÒN 250K 1 KHÓA HỌC BẤT KÌ, honamphoto.com HỖ TRỢ DỊCH COVID
Phụ huynh đăng ký mua khóa học lớp 6 cho con, được tặng miễn phí khóa ôn thi học kì. Cha mẹ hãy đăng ký học thử cho con và được tư vấn miễn phí. Đăng ký ngay!