Các phương pháp tính Value at Risk trong ngành ngân hàng
Lợi nhuận và rủi ro là 2 vấn đề mà ngành tài chính, especially banking quan tâm hàng đầu. Lợi nhuận thì ta có thể xác định rõ ràng. Còn rủi ro là khái niệm mơ hồ về định nghĩa nên càng rất khó để định lượng. Lúc còn sinh viên, mình đi ngang qua khoa Tài Chính FTU, thì nghe giảng viên dạy rằng rủi ro là mức độ dao động quanh giá trị dự kiến. Ví dụ khi bạn mua 1 cổ phiếu VNM giá 140.000 VND, bạn dự kiến ngày hôm sau giá là 150.000 VND, có thể dao động từ 130.000 VND đến 160.000 VND, thì đó là rủi ro. Tăng cao hơn dự kiến hoặc thấp hơn dự kiến đều được xem là rủi ro. Nghe có vẻ ổn, nhưng vẫn thấy không vừa lòng? Giá tăng thì càng tốt, thì làm sao mà xem là rủi ro được????
Kể từ đó, mình học ké các môn tài chính để hiểu thêm. Lúc đó giảng viên bắt đầu đưa ra công thức để đo rủi ro (Risk) bằng cách đo volatility (mức độ biến động): standard deviation. Sau khi tính ra Standard Deviation, ta sẽ so sánh hiệu quả các danh mục đầu tư bằng cách so sánh hệ số Sharp = (Expected Return – Risk-free Return)/ Standard deviation.
Đang xem: (Pdf) Ứng Dụng Value At Risk Là Gì ? Định Nghĩa
Mình thấy rằng, nhà đầu tư họ quan tâm đến rủi ro, nghĩa là họ lo sợ downturn risk (lo sợ giảm giá cổ phiếu), nghĩa là tình huống xấu, real return (hoặc loss) sẽ lệch so với Expected Return là bao nhiêu, trong 1 khoảng thời gian xác định. Chứ họ chả sợ là real return quá cao so với Expected Return haha. Khái niệm, khoảng return (hoặc mức thua lổ) trong x% tình huống xấu nhất, trong 1 khoảng thời gian gọi là Value at Risk (VaR).
Nghe qua, thì tính rủi ro theo VaR và tính rủi ro bằng mức độ biến động (Volatility: Standard Deviation) là 2 trường phái khác nhau. Nhưng thực tế là 1 khi ta giả định phân phối của Real Return là phân phối chuẩn, thì 2 cách tiếp cận này là 1. Lý do là vì nếu phân phối của Real Return là phân phối chuẩn, từ Standard Deviation ta có thể tính ra VaR và ngược lại. Tóm lại, trong tình huống lý tưởng, cả 2 cái này là 1, nhưng thực tế thì không lý tưởng.Ví dụ minh họa:Tôi mua cổ phiếu Vinamilk ngày hôm nay giá 140.000 VND. Tôi kỳ vọng giá là 158.000 VND vào năm sau.1. Kỳ vọng 158.000 VND, ở đâu tui ra số này?Kỳ vọng này tính ra bằng cách lấy giá trị tăng trưởng trung bình (average compound growth rate) của Vinamilk trong 10 năm qua. Tôi giả định năm nay sẽ tăng giá gần với tốc độ tăng trung bình trong 10 năm qua. Ví dụ tui tính ra 10 năm qua, trung bình mỗi năm VNM tăng giá 10%/ 1 năm.Expected Value = 140.000 + 140.000 x 10% = 158.000 VND.2. Rủi ro tui thua lỗ là bao nhiêu?Câu hỏi này chính xác là :”Sau một năm, xác xuất giá cổ phiếu thấp hơn 140.000 VND là bao nhiêu?”Ví dụ, tui tính ra Standard Deviation của Vinamilk trong năm qua là 15.000 VND. Giả định 1: Phân phối thực tế của cổ phiếu VNM là phân phối chuẩn. Nghĩa là giá VNM follow theo 1 đồ thị theo hình bên dưới: Các giá trị sẽ tập trung cao nhất quanh giá trị 158.000 VND. Càng về 2 bên (giá cao hơn hoặc thấp hơn 158.000 VND), xác xuất nhỏ dần (2 bên đều nhau).
Trong ví dụ này, ta tra bảng phân phối chuẩn và tính ra được xác xuất giá sau 1 năm thấp hơn 140.000 VND là 0.11507 (11.507%). Đó là VaR. Source.
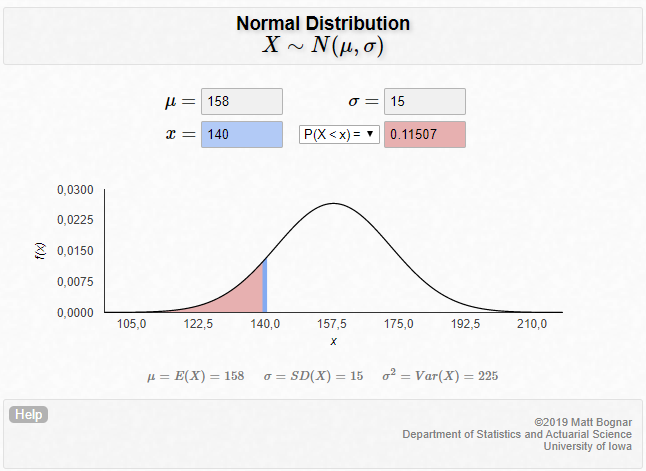
Đo Risk bằng cách đo Volatility thông qua Standard Deviation cũng tương đương đo Risk bằng VaR, với điều kiện Real Return có phân phối chuẩn (normal distribution) hay còn gọi là Gaussian distribution. Normal Distribution là assumption của việc dùng Standard Deviation để xác định Risk. Nhưng thực tế là giả định này failed.
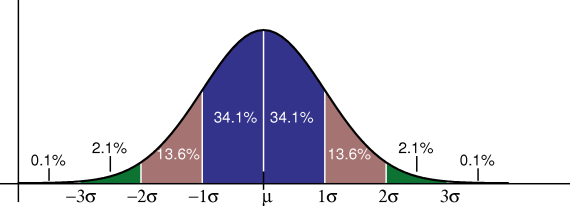
Normal distribution diagram (Source: Wikipedia)
Đặt điểm của phân phối chuẩn:Tính đối xứng qua trục MeanMean = Mode = DedianĐịnh lý giới hạn trung tâmTính ổn định của phân phối xác suất: Nếu là phân phối chuẩn, thì ta có thể suy luận từ Standard Deviation sang VaR với xác xuất cho trước và ngược lại.
Trong thực tế, phân phối của tỷ suất sinh lợi thực tế sẽ không tuân theo phân phối chuẩn. Phân phối thực tế sẽ bị biến thể theo 2 loại: Skewness và Kurtosis.
Skewness nghĩa là bị lệch: Medium > Mean > Mode hoặc Medium
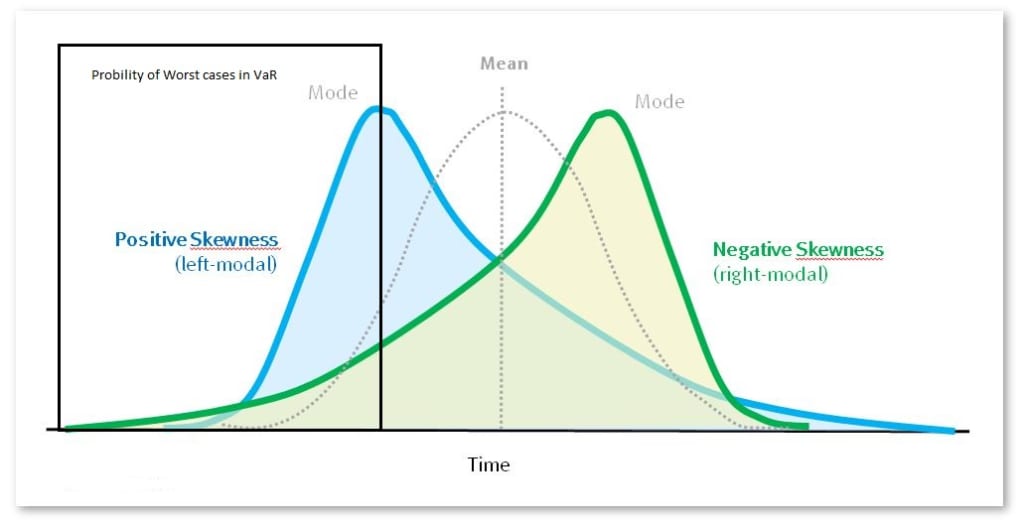
Xác xuất xảy ra tình huống xấu lớn hơn dự kiến với Positive Skewness.
Xem thêm: To Come In Nghĩa Là Gì ? Các Cụm Từ Với Come Come In Là Gì
Kurtosis là độ nhọn của phân phối. Excess kurtosis là sự chênh lệch giữ kurtosis của phân phối trừ đi kurtosis của phân phối chuẩn. Positive kurtosis (Leptokurtosis) là nguy hiểm, vì nó có xác suất giá trị extreme cao hơn xác xuất giá trị extreme của phân phối chuẩn.
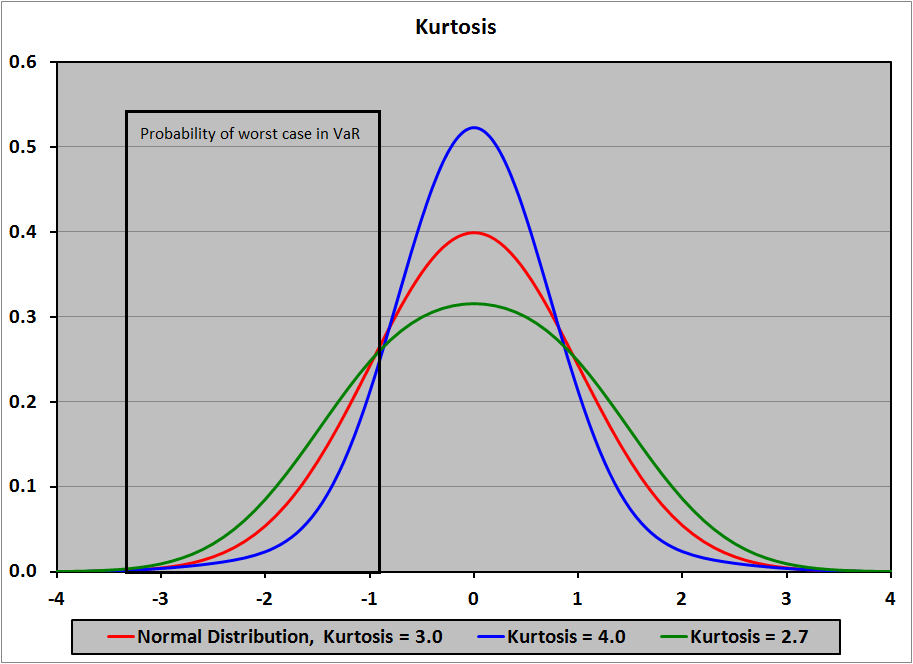
Xác xuất xảy ra tình huống xấu cao với Positive Kurtosis (Leptokutorsis) với xác xuất nhỏ.
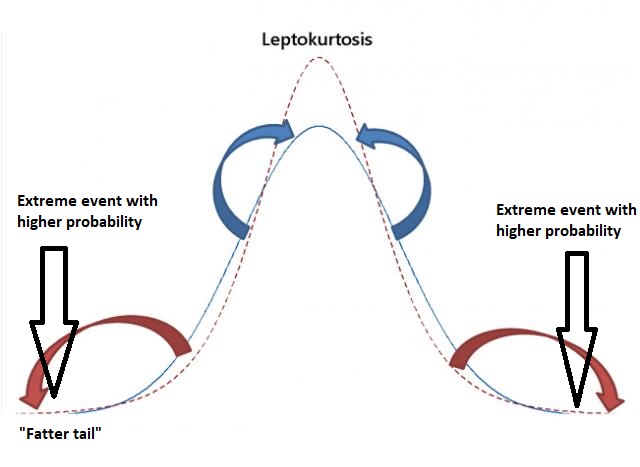
“Fat tail” distribution – Positive excess kurtosis – Leptokurtosis
Các nhóm phương pháp tính VaR – Value at Risk:Nhóm 1: ParametricGiả định của các phương pháp này là Real return sẽ tuân theo 1 quy luật phân phối nhất định, thường là chọn phân phối chuẩn.Variance-covariance VaR or delta-gamma VaRMục đích của việc đẻ ra Value at Risk là thay thế cho cách đo rủi ro bằng volatility. Nhưng phương pháp Parametric về bản chất lại không khác gì volatility, đều dựa trên giả định là phân phối chuẩn. Nên trong thực tế hầu như không có ngân hàng nào sử dụng phương pháp này.Nhóm 2: Non-parametricHistorical simulation VaRPhương pháp này có giả định là toàn bộ kết quả quá khứ sẽ lặp lại. Phương pháp này rất đơn giản, giả sử bạn có 100 kết quả lịch sử. Bạn muốn tìm VaR với confidence là 98%. Bạn xếp các giá trị lịch sử từ thấp đến cao, giá trị thứ 2 (100-98) chính là giá trị cần tìm. VaR = Giá trị trung bình (Mean) – Giá trị thứ 2.Ví dụ khác, giả sử bạn có 160 kết quả lịch sử. Bạn tìm VaR với Confidence là 99%. Số thứ tự bạn tính ra được là (1 – 99%)x160 = 1.6.Lúc này giá trị của số bạn cần tìm: Value = Giá trị số thứ 1 + 0.6x(Giá trị số thứ 2-Giá trị số thứ 1).Monte Carlo method VaRPhương pháp này loại bỏ hạn chế của Parametric Methods và Histrorical. Theo estimate của các bạn The McKinsey, 85% ngân hàng dùng historical simulation VaR và 15% các ngân hàng dùng Monte Carlo method.
Mình đã tính và test thử phương pháp Monte Carlo Simulation. Phân phối của kết quả chạy 20.000 lần là Phân Phối Highly Positive Excess Skewness và Leptokurtosis. Vậy là rõ ràng Monte Carlo đã khắc phục được các nhược điểm của Historical Simulation và các Phương Pháp Parametric truyền thống (Varian-Covarian VaR). Kết quả là các giá trị Var với confidence là 99%; 98%; 90%; 20% rất ổn định, sai biệt giữa các lần reset là dưới 1%.Với số lần lặp là 20.000 lần thì kết quả tuân theo quy luật số lớn mạnh. Giá trị trung bình tiệm cận giá trị kì vọng, sai lệch 0.3% giữa các lần reset.

Expected Shotfall (ES) – Conditional VaR (CVaR)Sau khi tính VaR xong, họ còn kỹ lưỡng hơn để tính giá trị rủi ro bằng Expected Shotfall (ES) hay còn gọi là Conditional Value at Risk (CVaR).Giả sử danh mục của bạn có 1.000 biến cố xảy ra, bạn xếp các giá trị của danh mục từ thấp đến cao. Khi tính VaR với level of confidence là 99%, Giá tri thứ 10 chính là giá trị bạn lấy. Tuy nhiên, với CVaR, bạn sẽ tính trung bình cộng của các giá trị theo số thứ tự từ 1 đến 10, sau đó dùng kết quả này so sánh với mean của 1.000 biến cố để tính CVaR. Ý nghĩa của Expected Shotfall Khi xảy ra các biến cố nằm ngoài khoảng tin cậy (level of confidence), thì giá trị dự kiến của các biến cố này sẽ hội tụ về giá trị trung bình theo quy luật số lớn. Cụ thể ở ví dụ trên, với condition là biến cố nằm ngoài 99%, nghĩa là khi xảy ra 1% xấu nhất, thì giá trị trung bình của các biến cố xấu nhất sẽ có xác suất xảy ra cao nhất.Expected Shotfall (ES) hay còn gọi là CVaR giúp khắc phục 2 hạn chế của Value at Risk (VaR).i. Tổng giá trị VaR thành phần không chắc là bằng giá trị VaR của Portfolio. Tuy nhiên, CVaR lại khắc phục hạn chế này. Nghĩa là CVaR của Portfolio bằng tổng các giá trị riệng lẻ của các CVaR của tài sản thành phần.ii. VaR chưa tính đến chuyện khi xảy ra tình huống xấu nhất, thì giá trị của danh mục sẽ rơi vào đâu. CVaR thì hoàn toàn giải quyết được bài toán này theo quy luật số lớn – The Law of Large Numer (LLN).
Xem thêm: Kiểm Tra Thông Tin Của Một Tài Khoản Google Của Tôi Là Gì, Giới Thiệu Về Tài Khoản Google
Từ phương pháp tính Expected Shotfall, mình thấy rằng, với level of confidence càng lớn, thì khi xảy ra biến cố ngoài mong đợi, tổn thất sẽ càng lớn.