Bảng phân phối Student hay còn gọi là phân phối t được ứng dụng trong nhiều môn học đại cương của các ngành kinh tế học như: Xác suất thống kê, kinh tế lượng,… Dưới đây là bảng phân phối Student chính xác kèm theo một số lý thuyết cơ bản và bài tập vận dụng.
Đang xem: Hướng dẫn cách tra bảng student
Phân phối Student là gì?
Phân phối Student còn được gọi là phân phối T hay phân phối T Student, trong tiếng anh là T Distribution hay Student’s t-distribution.
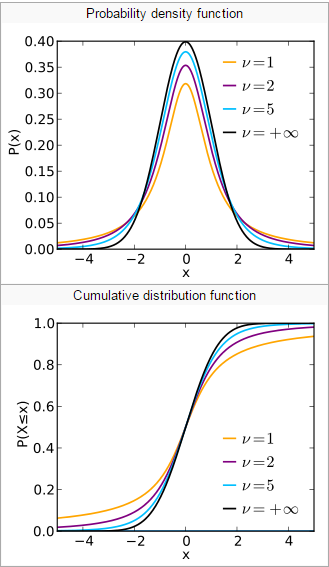
Phân phối Student có hình dạng đối xứng trục giữa gần giống với phân phối chuẩn. Khác biệt ở chỗ phần đuôi nếu trường hợp có nhiều giá trị trung bình phân phối xa hơn sẽ khiến đồ thị dài và nặng. Phân phối student thường ứng dụng để mô tả các mẫu khác nhau trong khi phân phối chuẩn lại dùng trong mô tả tổng thể. Do đó, khi dùng để mô tả mẫu càng lớn thì hình dạng của 2 phân phối càng giống nhau
Bảng phân phối Student PDF
1. Bảng phân phối Student
| Bậc tự do (df) | p-value | 0.25 | 0.2 | 0.15 | 0.1 | 0.05 | 0.025 | 0.02 | 0.01 | 0.005 | 0.0025 | 0.001 | 0.0005 |
| 1 | 1 | 1.376 | 1.963 | 3.078 | 6.314 | 12.71 | 15.89 | 31.82 | 63.66 | 127.3 | 318.3 | 636.6 |
| 2 | 0.816 | 1.061 | 1.386 | 1.886 | 2.92 | 4.303 | 4.849 | 6.965 | 9.925 | 14.09 | 22.33 | 31.6 |
| 3 | 0.765 | 0.978 | 1.25 | 1.638 | 2.353 | 3.182 | 3.482 | 4.541 | 5.841 | 7.453 | 10.21 | 12.92 |
| 4 | 0.741 | 0.941 | 1.19 | 1.533 | 2.132 | 2.776 | 2.999 | 3.747 | 4.604 | 5.598 | 7.173 | 8.61 |
| 5 | 0.727 | 0.92 | 1.156 | 1.476 | 2.015 | 2.571 | 2.757 | 3.365 | 4.032 | 4.773 | 5.893 | 6.869 |
| 6 | 0.718 | 0.906 | 1.134 | 1.44 | 1.943 | 2.447 | 2.612 | 3.143 | 3.707 | 4.317 | 5.208 | 5.959 |
| 7 | 0.711 | 0.896 | 1.119 | 1.415 | 1.895 | 2.365 | 2.517 | 2.998 | 3.499 | 4.029 | 4.785 | 5.408 |
| 8 | 0.706 | 0.889 | 1.108 | 1.397 | 1.86 | 2.306 | 2.449 | 2.896 | 3.355 | 3.833 | 4.501 | 5.041 |
| 9 | 0.703 | 0.883 | 1.1 | 1.383 | 1.833 | 2.262 | 2.398 | 2.821 | 3.25 | 3.69 | 4.297 | 4.781 |
| 10 | 0.7 | 0.879 | 1.093 | 1.372 | 1.812 | 2.228 | 2.359 | 2.764 | 3.169 | 3.581 | 4.144 | 4.587 |
| 11 | 0.697 | 0.876 | 1.088 | 1.363 | 1.796 | 2.201 | 2.328 | 2.718 | 3.106 | 3.497 | 4.025 | 4.437 |
| 12 | 0.695 | 0.873 | 1.083 | 1.356 | 1.782 | 2.179 | 2.303 | 2.681 | 3.055 | 3.428 | 3.93 | 4.318 |
| 13 | 0.694 | 0.87 | 1.079 | 1.35 | 1.771 | 2.16 | 2.282 | 2.65 | 3.012 | 3.372 | 3.852 | 4.221 |
| 14 | 0.692 | 0.868 | 1.076 | 1.345 | 1.761 | 2.145 | 2.264 | 2.624 | 2.977 | 3.326 | 3.787 | 4.14 |
| 15 | 0.691 | 0.866 | 1.074 | 1.341 | 1.753 | 2.131 | 2.249 | 2.602 | 2.947 | 3.286 | 3.733 | 4.073 |
| 16 | 0.69 | 0.865 | 1.071 | 1.337 | 1.746 | 2.12 | 2.235 | 2.583 | 2.921 | 3.252 | 3.686 | 4.015 |
| 17 | 0.689 | 0.863 | 1.069 | 1.333 | 1.74 | 2.11 | 2.224 | 2.567 | 2.898 | 3.222 | 3.646 | 3.965 |
| 18 | 0.688 | 0.862 | 1.067 | 1.33 | 1.734 | 2.101 | 2.214 | 2.552 | 2.878 | 3.197 | 3.611 | 3.922 |
| 19 | 0.688 | 0.861 | 1.066 | 1.328 | 1.729 | 2.093 | 2.205 | 2.539 | 2.861 | 3.174 | 3.579 | 3.883 |
| 20 | 0.687 | 0.86 | 1.064 | 1.325 | 1.725 | 2.086 | 2.197 | 2.528 | 2.845 | 3.153 | 3.552 | 3.85 |
| 21 | 0.686 | 0.859 | 1.063 | 1.323 | 1.721 | 2.08 | 2.189 | 2.518 | 2.831 | 3.135 | 3.527 | 3.819 |
| 22 | 0.686 | 0.858 | 1.061 | 1.321 | 1.717 | 2.074 | 2.183 | 2.508 | 2.819 | 3.119 | 3.505 | 3.792 |
| 23 | 0.685 | 0.858 | 1.06 | 1.319 | 1.714 | 2.069 | 2.177 | 2.5 | 2.807 | 3.104 | 3.485 | 3.768 |
| 24 | 0.685 | 0.857 | 1.059 | 1.318 | 1.711 | 2.064 | 2.172 | 2.492 | 2.797 | 3.091 | 3.467 | 3.745 |
| 25 | 0.684 | 0.856 | 1.058 | 1.316 | 1.708 | 2.06 | 2.167 | 2.485 | 2.787 | 3.078 | 3.45 | 3.725 |
| 26 | 0.684 | 0.856 | 1.058 | 1.315 | 1.706 | 2.056 | 2.162 | 2.479 | 2.779 | 3.067 | 3.435 | 3.707 |
| 27 | 0.684 | 0.855 | 1.057 | 1.314 | 1.703 | 2.052 | 2.158 | 2.473 | 2.771 | 3.057 | 3.421 | 3.69 |
| 28 | 0.683 | 0.855 | 1.056 | 1.313 | 1.701 | 2.048 | 2.154 | 2.467 | 2.763 | 3.047 | 3.408 | 3.674 |
| 29 | 0.683 | 0.854 | 1.055 | 1.311 | 1.699 | 2.045 | 2.15 | 2.462 | 2.756 | 3.038 | 3.396 | 3.659 |
| 30 | 0.683 | 0.854 | 1.055 | 1.31 | 1.697 | 2.042 | 2.147 | 2.457 | 2.75 | 3.03 | 3.385 | 3.646 |
| 40 | 0.681 | 0.851 | 1.05 | 1.303 | 1.684 | 2.021 | 2.123 | 2.423 | 2.704 | 2.971 | 3.307 | 3.551 |
| 50 | 0.679 | 0.849 | 1.047 | 1.299 | 1.676 | 2.009 | 2.109 | 2.403 | 2.678 | 2.937 | 3.261 | 3.496 |
| 60 | 0.679 | 0.848 | 1.045 | 1.296 | 1.671 | 2 | 2.099 | 2.39 | 2.66 | 2.915 | 3.232 | 3.46 |
| 80 | 0.678 | 0.846 | 1.043 | 1.292 | 1.664 | 1.99 | 2.088 | 2.374 | 2.639 | 2.887 | 3.195 | 3.416 |
| 100 | 0.677 | 0.845 | 1.042 | 1.29 | 1.66 | 1.984 | 2.081 | 2.364 | 2.626 | 2.871 | 3.174 | 3.39 |
| 1000 | 0.675 | 0.842 | 1.037 | 1.282 | 1.646 | 1.962 | 2.056 | 2.33 | 2.581 | 2.813 | 3.098 | 3.3 |
| z* | 0.674 | 0.841 | 1.036 | 1.282 | 1.645 | 1.96 | 2.054 | 2.326 | 2.576 | 2.807 | 3.091 | 3.291 |
| Khoảng tin cậy (CI) | 50% | 60% | 70% | 80% | 90% | 95% | 96% | 98% | 99% | 99.50% | 99.80% | 99.90% |
Ghi chú: Khoảng tin cậy là CI = > $alpha $ = 1 -CI
2. File PDF
Ứng dụng
Phân phối T – Student thường được dùng rộng rãi trong việc suy luận phương sai tổng thể khi có giả thiết tổng thể phân phối chuẩn, đặc biệt khi cỡ mẫu càng nhỏ thì độ chính xác càng cao. Ngoài ra, còn được ứng dụng trong kiểm định giả tiết về trung bình khi chưa biết phương sai tổng thể là bao nhiêu.
Xem thêm: Vi Khuẩn Kỵ Khí Là Gì – Các Bệnh Nhiễm Khuẩn Do Vi Khuẩn Kỵ Khí
Phân phối này được ứng dụng trong cả xác suất thống kê và kinh tế lượng.
Các tính chất
Nếu như $Y sim N(0,1)$, $Z sim {X^2}(k)$ và độc lập với $Y$ thì $X = frac{Y}{{sqrt {frac{Z}{k}} }} sim T(k)$. Trong trường hợp này phân phối Student có:
Hình dạng đối xứng gần giống phân phối chuẩn hóaKhi cỡ mẫu càng lớn càng giống phân phối chuẩn hóaCỡ mẫu càng nhỏ, phần đuôi càng nặng và xa hơn
Hàm mật độ: $f(x) = frac{{Tleft( {frac{{k + 1}}{2}}
ight)}}{{sqrt {pi k} Tleft( {frac{k}{2}}
ight){{left( {1 + frac{{{x^2}}}{k}}
ight)}^{frac{{k + 1}}{2}}}}};x in R$
Trung bình: $mu = 0$
Phương sai: ${sigma ^2} = frac{k}{{k – 2}},k ge 2$
Cách tra bảng phân phối Student
Để tìm hiểu chi tiết về cách tra, mình giới thiệu đến các bạn ví dụ sau: Giả sử một cỡ mẫu có $n = 41$, độ tin cậy $90\% $. Tra bảng $t(n – 1)$ bằng bao nhiêu với $frac{alpha }{2}$
Giải:
Độ tin cậy: $gamma = 90\% Rightarrow 1 – alpha = 0.9 Rightarrow frac{alpha }{2} = 0.05$
Với $n = 41 Rightarrow df = n – 1 = 40$
Khi đó: $tleft< {(n – 1),frac{alpha }{2}} ight> = t(40,0.05) = 1.684$
Bài tập vận dụng
Cho một mẫu với cỡ mẫu là $n = 32$, giá trị trung bình $mu = 128.5$. Sai số chuẩn $SE = 6,2$. Tìm khoảng tin cậy ${99\% }$ của giá trị trung bình.
Giải
Tóm tắt đề: $n = 32,mu = 128.5,SE = 6,2,CI(99\% ) = ?$
Ta có: $df = n – 1 = 31$
$frac{alpha }{2} = frac{{1 – 99\% }}{2} = 0.005$
Suy ra: $t(31,0.005) = 2,744$
Vậy: $CI(99\% ) = (mu – SE.t;mu + SE.t) = (111,5;145,5)$
Lưu ý
Trong quá trình ứng dụng bảng phân phối Student trong xác suất thống kê và các bộ môn liên quan cần lưu ý:
Sử dụng bảng phân phối chính xácPhân biệt các khái niệm về: Độ tin cậy, độ lệch chuẩnNên tóm tắt đề trước khi giải toán