Lớp 1
Lớp 2
Lớp 2 – Kết nối tri thức
Lớp 2 – Chân trời sáng tạo
Lớp 2 – Cánh diều
Tài liệu tham khảo
Lớp 3
Sách giáo khoa
Tài liệu tham khảo
Sách VNEN
Lớp 4
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Lớp 5
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Lớp 6
Lớp 6 – Kết nối tri thức
Lớp 6 – Chân trời sáng tạo
Lớp 6 – Cánh diều
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 7
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 8
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 9
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 10
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 11
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 12
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
IT
Ngữ pháp Tiếng Anh
Lập trình Java
Phát triển web
Lập trình C, C++, Python
Cơ sở dữ liệu

Chuyên đề Toán 9Chuyên đề: Hệ hai phương trình bậc nhất hai ẩnChuyên đề: Phương trình bậc hai một ẩn sốChuyên đề: Hệ thức lượng trong tam giác vuôngChuyên đề: Đường trònChuyên đề: Góc với đường trònChuyên đề: Hình Trụ – Hình Nón – Hình Cầu
Dạng bài tập Tìm giá trị của biến để biểu thức có giá trị nguyên cực hay
Trang trước
Trang sau
Dạng bài tập Tìm giá trị của biến để biểu thức có giá trị nguyên cực hay
Phương pháp giải
a) Tìm x nguyên để biểu thức A =
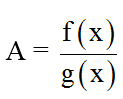
nguyên.
Đang xem: Dạng Toán Tìm X Để A Nguyên Để A Nhận Giá Trị Nguyên
Bước 1. Tách A thành dạng
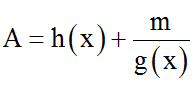
trong đó h(x) là một biểu thức nguyên khi x nguyên, m là nguyên.
Bước 2: A nguyên ⇔
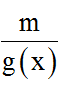
nguyên ⇔ g(x) ∈ Ư(m).
Bước 3. Với mỗi giá trị của g(x), tìm x tương ứng và kết luận.
b) Tìm x để biểu thức A nguyên (Sử dụng phương pháp kẹp).
Bước 1: Áp dụng các bất đẳng thức để tìm hai số m, M sao cho m Hiển thị đáp án
Đáp án: C
Bài 2: Có bao nhiêu giá trị nguyên của x để biểu thức
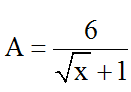
nguyên?
A. 3B. 4C. 6D. 8
Hiển thị đáp án
Đáp án: B
Bài 3: Có tất cả bao nhiêu giá trị nguyên của x để biểu thức
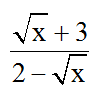
nguyên?
A. 2B. 3C. 4D. 5
Hiển thị đáp án
Bài 4: Với tất cả các số nguyên x, giá trị nguyên lớn nhất của biểu thức
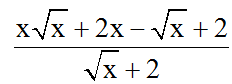
là:
A. 1B. 2C. 3D. 4
Hiển thị đáp án
Đáp án: D
Bài 5: Có bao nhiêu giá trị của x để biểu thức
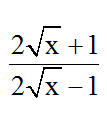
nguyên?
A. 2B. Vô sốC. 3D. 1
Hiển thị đáp án
Đáp án: B
Bài 6: Tìm các giá trị nguyên của x để các biểu thức dưới đây nguyên:
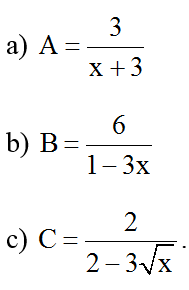
Hướng dẫn giải:
a) Đkxđ: x ≠ -3.
A ∈ Z ⇔ ⇔ x + 3 ∈ Ư(3) = {-3; -1; 1; 3} ⇔ x ∈ {-6; -4; -2; 0}
b) Đkxđ: x ≠ 1/3 .
B ∈ Z ⇔
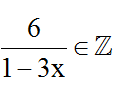
⇔ 1 – 3x ∈ Ư(6) = {-6; -3;-2; -1; 1; 2; 3; 6}
Ta có bảng:

Trong các giá trị trên, chỉ có x = 1 hoặc x = 0 thỏa mãn x nguyên.
Vậy x = 0 hoặc x = 1.
c)
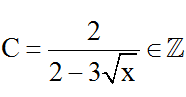
⇔ 2 – 3√x ∈ Ư(2) = {-2; -1; 1; 2}
Ta có bảng sau:
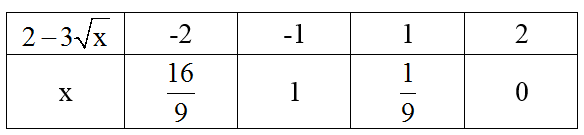
Trong các giá trị trên chỉ có x = 1 hoặc x = 0 thỏa mãn.
Vậy x = 0 hoặc x = 1.
Bài 7: Tìm các giá trị nguyên của x để các biểu thức dưới đây nguyên:

Hướng dẫn giải:
a)
Đkxđ: x ≥ 0; x ≠ 4 .
Ta có:
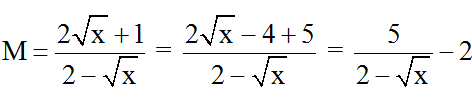
.
M ∈ Z ⇔
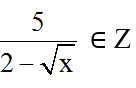
∈ Z ⇔ 2 – √x ∈ Ư(5) = {-5; -1; 1; 5}.
Ta có bảng:

Vậy với x ∈ {49; 9; 1} thì biểu thức M có giá trị nguyên.
b)
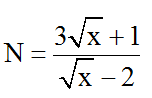
Đkxđ: x ≥ 0 ; x ≠ 4 . Ta có:
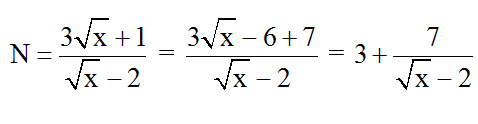
N ∈ Z ⇔
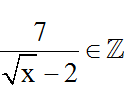
⇔ √x – 2 Ư(7) = {-7; -1; 1; 7}.
Ta có bảng sau:

Vậy với x ∈ {1; 9; 81} thì biểu thức nhận giá trị nguyên.
Bài 8: Tìm các giá trị của x để các biểu thức
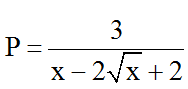
nguyên
Hướng dẫn giải:
Điều kiện: x ≥ 0 .
Ta có: x – 2√x + 2 = x – 2√x + 1 + 1 = (√x – 1)2 + 1 ≥ 1 > 0
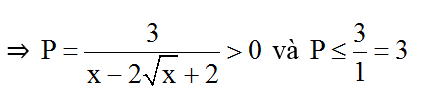
⇒ 0 2 = -3/4 2 = -8/9 0 với mọi x.
⇒ 0 0; x ≠ 1.
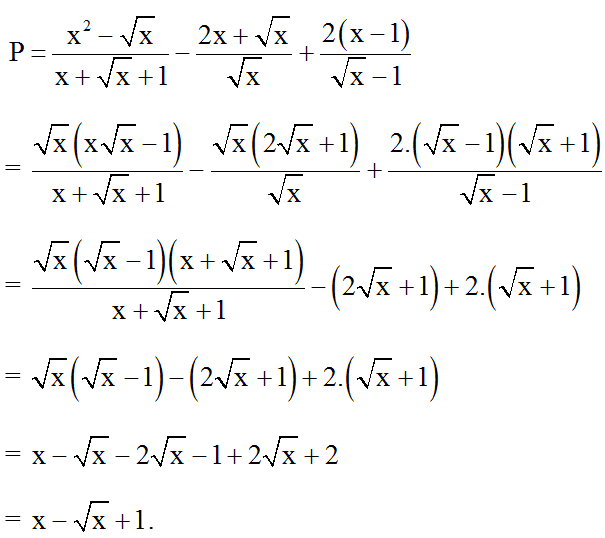
b) Ta có:
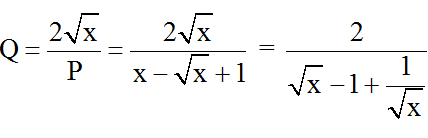
Áp dụng bất đẳng thức Cô-si ta có:
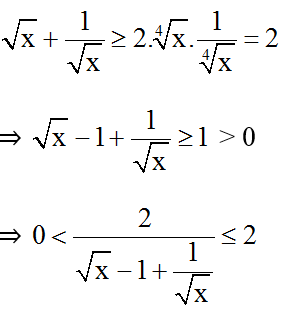
Mục lục các Chuyên đề Toán lớp 9:
Chuyên đề Đại Số 9Chuyên đề Hình Học 9
CHỈ CÒN 250K 1 KHÓA HỌC BẤT KÌ, honamphoto.com HỖ TRỢ DỊCH COVID
Phụ huynh đăng ký mua khóa học lớp 9 cho con, được tặng miễn phí khóa ôn thi học kì. Cha mẹ hãy đăng ký học thử cho con và được tư vấn miễn phí. Đăng ký ngay!